Work with a professional finance tutor in London or online
Finance Tutor in London for Corporate Finance, Financial Markets, Financial Management, Financial Economics. Senior finance tutors from LSE, UCL, Kings, Cambridge, Oxford University students. Get 1-on-1 or Online Finance Tutoring lessons.

Option as Derivatives
The figure above shows a call option payoff graphs. Options are derivatives instruments. A derivative is a financial instrument whose value is ‘derived’ from the underlying asset. In this case, the option is on an underlying equity (stock). A call option gives the buyer (holder) of the option the right to buy the asset (stock) at a pre-determined strike price (also called exercise price). The option also has a maturity or time-frame within which it is valid.
To summarize: S0 = is current stock price, St= stock price at expiry, X = Exercise price at which holder of call option can buy the stock T = Maturity of the option, rf= risk free interest rate
Call Option
A Call option gives the owner the right to buy a security. In the graph above, the strike price is $20. As long as the stock price is below $20 at maturity/expiry of the option the option expires worthless. That is, if the stock is trading at $18 in the market, the holder of the option will not pay $20 to buy it by exercising the option. Therefore, the option expires without being exercised and is worthless to the holder of the option.
Consider, if the stock is trading at $22 on maturity date the owner of the option will benefit from exercising it. In this case the owner will buy the stock at $20 which is worth $22 in the market, giving him a payoff of $2. The payoff from a call option is thus given by Max{ St – X, 0}. This formula implies that the payoff will be the larger value of 0 and a positive number. Option payoff can thus never be negative. Buyer of a call option profits when the stock price goes up. Put differently, a buyer of a call option bets of the stock price to goes up. Work with our finance tutor in London for an in-depth understanding of pricing and payoffs of call options.
Put Option

The figure above shows a put option payoff in red and a call option payoff in blue. Put option is a right to sell an asset at a pre-determined strike price. Buyer of the put options profits when the stock price declines. In other words, a put option buyer is betting stock price to go down. Finance tutor in London will cover Put-Call parity in detail.
This question is about option pricing
The current price of stock XYZ is £100, and each month it either goes up by 15% or goes down by 10%. The monthly riskless interest rate is 5%. Assume that the stock does not pay dividends. Our finance tutor in London can practice similar questions for courses like corporate finance, financial management, and financial markets.
- Construct a binomial tree with three dates 0, 1, and 2 for stock price movements and calculate risk neutral probabilities of the up and down moves.
- Calculate the time-0 price of a European call with strike price of £100 and maturity at date 2.
- Determine the delta of the call option in part b) at time zero. Using put-call parity determine the time-0 price of a put option with strike price £100, which matures at date 2.
- What is the price of a bull spread with strikes and maturing at date 2? Assume that the price movements of the stock are described by the binomial tree in part a). (Hint: a bull spread is constructed as a long position in one European call with strike Kl and a short position in one European call with strike ).
- Consider a European security, which pays at the terminal date . That is, the payoff is the minimum of two numbers: stock price and . Assume that Plot the payoff diagram. Construct a portfolio of stocks and call options, which replicates the payoff of this security at date .
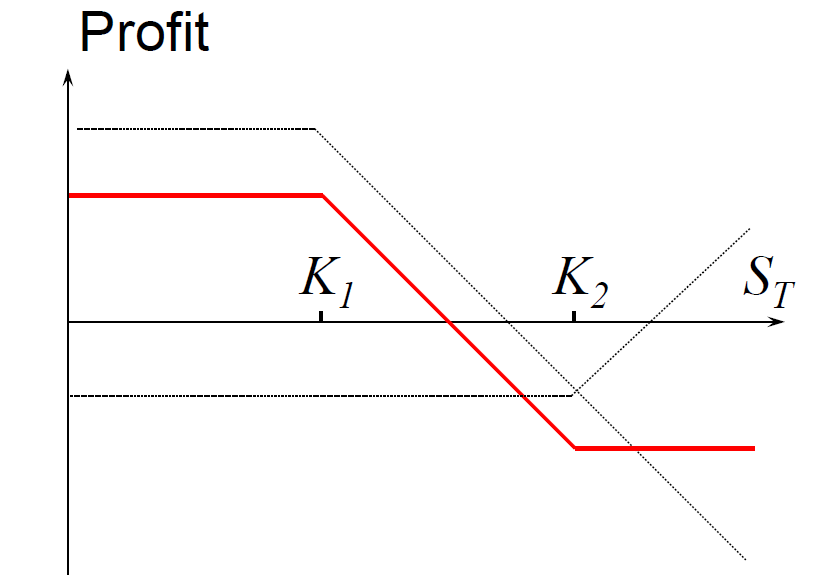
Bear spread using call options
We can also combine multiple options to create exposures suitable for our views. For example a bear spread is a strategy used to gain from downside. We can sell a call at a lower strike price (K1) and buy a call at a higher strike price (K2). The diagram below shows the payoff of a bear spread. Can you write an expression for the payoff with a short call at K1 and a long call at K2? Our finance tutor in London will go over commonly used option strategies such as bear spread, box spread, collar, butterfly, straddle, and strangle.
Work with a qualified finance tutor in London or online for FM212/FM213/FM473.
Financial_Statements_Taxes_and_Cash_Flow
Discounted_Cash_Flow_Valuation_(Part_I)
Discounted_Cash_Flow_Valuation_(Part_II)
Interest_Rate_and_Bond_Valuation
Finance Exam 2013 Finance Exam 2014 Finance Exam Sample Paper Finance Tutor London Exam Sample II
EconTutor has tutors available for these courses
- Microeconomics
- Macroeconomics
- MBA Economics
- Econometrics
- Statistics
- Quantitative Finance tutors
- Principles of Finance
- Mathematical Finance
- FM212 Finance Tutor LSE
- FM473 Financial Markets Tutor LSE
- FM474 Managerial Finance Tutor LSE
- SMN 224 Corporate Finance Tutor for Kings College
- Finance for Real Estate
- Finance for Private Equity
- MBA Finance Courses
- Financial Economics
- Reviews
- Financial Econometrics
Our tutors are available in Central London, North London, Manchester, Birmingham, Oxford, Bristol, Cambridge, Liverpool, Newcastle, Cardiff, Reading, Durham, Leicester, Lancaster, Sheffield. Book a free lesson with our Finance Tutor London.
