Econometrics Tutor Bristol- Econometrics I & II, Time Series Econometrics

Experienced Econometrics Tutor for Bristol University Econometrics courses.

econometrics tutor bristol university

Rendered by QuickLaTeX.com

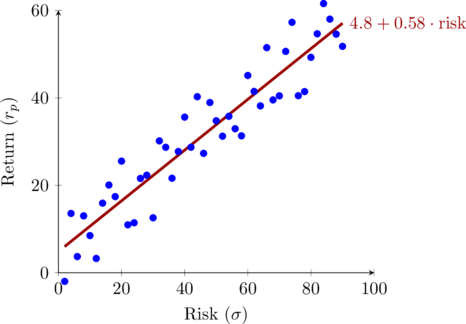
CLRM Assumptions

$E[\epsilon]=0$ holds whenever there is an intercept, it means the error term is zero, on average.
No perfect multicollinearity and all Xs must exhibit some variation (MLR)
- *No perfect linear relationship between the Xs
- *The higher the variation in independent variables, the lower the variance of estimators. To increase variation, increase the sample size.
Conditional independence assumption
- $E[\epsilon| X_1, X_2, ..., X_k]=E[\epsilon] =0$
- If this holds, there is no selection effect. (observed effect = causal effect)
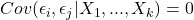$Cov(\epsilon_i, \epsilon_j | X_1, ..., X_k) =0$ Zero serial correlation in the errors
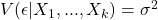$V(\epsilon | X_1, ... ,X_k) = \sigma^2$ homoskedasticity, or constant conditional variance of the residual term
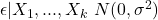$\epsilon | X_1, ... , X_k ~ N (0, \sigma^2)$ errors are normally distributed with a mean zero and constant variance.

Microeconomics and Macroeconomics tutors in Bristol.

Best 1-on-1 Econometrics tutors for Bristol University – available in-person and online. Our tutors are experts in topics such as classical linear regression model, multiple regression, Gauss Markov assumptions, dummy variables, fixed effects, random effects, instrumental variables, logit and probit models. Advanced Time series and econometric theory tutors also available.

Taking too long?

Reload document

Open in new tab

Econometrics Tutor Bristol University

Bristol Economics Tutorial Lecture I

Econometrics I, Econometrics II, Econometrics Theory, Time Series Econometrics, Financial Econometrics, Econometrics for Management, Statistics and Econometrics

Question A

Suppose one is interested in measuring the impact of participation in preschool between ages 0 and 3 (P_i a dummy variable which takes value 1 if an individual ever participated in preschool between the ages of O and 3, and which takes value O otherwise) on mathematics test scores measured at age 12 (M_i). Therefore, one could think of running the following regression:

In a given dataset where we observe M and P for a cross section of individuals, should we expect P and u to be uncorrelated? Explain your answer. Should we expect the OLS estimate of β to be unbiased? Explain. [6 points]
What is the expression of the estimator for βif you use the procedure you described in part 2 of this question. Is it unbiased? If yes, show why. If not, show the expression for the [6 points]
Suppose now that compliance with the lottery was perfect, which means that every child offered a place accepted it, and none of the children rejected in the public sector ever enrolled in preschool. Would you be able to get an unbiased estimate of β estimating the model in part 1 of this question? Why, or why not? [5 points]

Book a free trial lesson with our Econometrics Tutor in Bristol University for a complete lesson plan.

Other popular courses: